Tipos de funções

 

             Aluna: Aislin Gabriella dos Santos Campos.             Turma: 18122.1M

          

          Blog realizado como requisito aliativo da matéria de matemática, III unidade, ministrado pelo prof. Mateus Souza de Oliveira.😁

TIPOS DE FUNCÕES

Vamos estudar agora quando uma função é sobrejetora, injetora ou bijetora. 

Função injetora: 

• Uma função f é injetora quando não existe elemento do contra domínio que seja imagem de mais de um elemento do domínio da função.

Função sobrejetora

• Uma função f é sobrejetora quando todo elemento do contradomínio é imagem pelo menos de um elemento do domínio da função.

 

Função bijetora 

• Uma função f: A → B é bijetora quando é sobrejetora e injetora ao mesmo tempo.

FUNÇÃO COMPOSTA

• é a aplicação de uma função em outra função, conhecida também como função de função. Dada a função f: A → B e g: B → C, a função composta de f com g pode ser presentada por fog: A → C, que nada mais é que a composição f(g(x)).

COMO CALCULAR FUNÇÃO COMPOSTA?

• Para encontrar a lei de formação da função composta fog(x), basta lembrar que fog = f(g(x)). Sendo assim, substitui-se as variáveis da função f pela lei de formação da função g(x).

Exemplo 1:

Dadas as funções de f e g R → R, com lei de formação f(x) = 2x + 3 e g(x) = x² + 5x – 4, encontre:

a) fog(x)

b) gof(x)

Resolução:

a) Para encontrar fog(x), substituiremos a variável de f(x) pela lei de formação de g(x), então encontraremos f(g(x)).

Sabemos que:

f(x) = 2x + 3 e g(x) = x² + 5x – 4

f(g(x)) = 2(x² + 5x – 4) + 3

Aplicaremos a propriedade distributiva para eliminar os parênteses:

f(g(x)) = 2x² + 10x – 8 + 3

Então, temos que:

f(g(x)) = 2x² + 10x – 5

b) Agora, encontraremos gof(x).

Sabemos que:

g(x) = x² + 5x – 4 e f(x) = 2x + 3

Então, temos que:

g(f(x)) = (2x + 3)² + 5(2x + 3) – 4

g(f(x)) = (2x + 3) (2x + 3) + 10x + 15 – 4

g(f(x)) = 2x² + 6x + 6x + 9 + 10x + 15 – 4

g(f(x)) = 4x² + 22x + 20

FUNÇÃO INVERSA

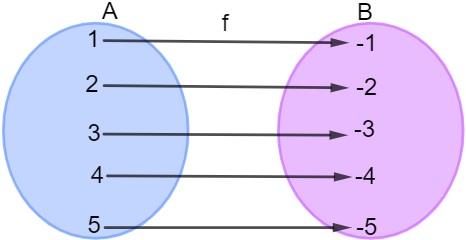
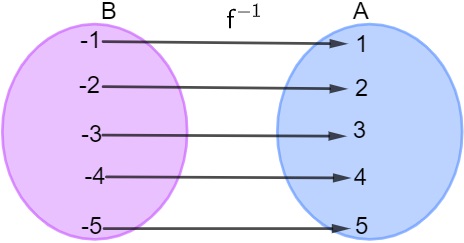
• Como o nome já sugere, é a função f(x)^-1, que faz exatamente o inverso da função f(x).

• Para que uma função admita uma inversa, ela precisa ser bijetora, ou seja, injetora e sobrejetora ao mesmo tempo.

•  A lei de formação de uma função inversa faz o contrário do que a função f(x) faz.
• Por exemplo, se a função pega um valor do domínio e soma 2, a função inversa, ao invés de somar, subtrai. 
•  Encontrar a lei de formação da função inversa nem sempre é uma tarefa fácil, sendo necessário inverter as incógnitas x e y, bem como isolar y na nova equação

Quando uma função admite inversa?

• Uma função é inversível, ou seja, possui função inversa, se, e somente se, ela for bijetora. É importante lembrarmos o que é uma função bijetora, que é uma função injetora, ou seja, todo elemento da imagem possui um único correspondente no domínio.
• Uma função é sobrejetora se a imagem for igual ao contradomínio

Exemplo 2:

• A função f : A → B é bijetora, pois ela é injetora (afinal, elementos distintos em A estão associados a elementos distintos em B) e também é sobrejetora, pois não sobra nenhum elemento no conjunto B, ou seja, o contradomínio é igual ao conjunto imagem.

Assim sendo, essa função é inversível, e a sua inversa é:

Como se determina a lei de formação da função inversa?

• Para encontrar a lei de formação da função inversa, precisamos inverter as incógnitas, ou seja, trocar x por y e y por x, e posteriormente isolar a incógnita y. Para isso, é importante que a função seja inversível, ou seja, bijetora.

 Exemplo 3:

Encontre a lei de formação da função inversa de f(x) = x + 5.

Resolução:

Sabemos que f(x) = y, então y = x + 5. Realizando a inversão de x e y, vamos encontrar a seguinte equação:

x = y + 5

Agora, vamos isolar o y:

– 5 + x = y
y = x – 5

É evidente que, se f(x) soma 5 ao valor de x, então a sua inversa f(x) ^{- 1} fará o inverso, ou seja, x menos 5.

TODAS AS REFEENCIAS DA TERCEIRA PARTE:

https://matematicario.com.br/blog/funcao-o-que-e-tipos-de-funcoes-e-graficos/#:~:text=Tipos%20de%20fun%C3%A7%C3%A3o,e%20fun%C3%A7%C3%A3o%20bijetora%20ou%20bijetiva.
https://mundoeducacao.uol.com.br/matematica/funcao-composta.htm#:~:text=Fun%C3%A7%C3%A3o%20composta%20%C3%A9%20a%20aplica%C3%A7%C3%A3o,f(g(x)).
https://www.educamaisbrasil.com.br/enem/matematica/funcao-logaritmica
https://www.todamateria.com.br/funcao-exponencial/
https://brasilescola.uol.com.br/matematica/funcao-inversa.htm
Livro de matemática
meu caderno