Funções Logarítmicas (concluido)
Aluna: Aislin Gabriella dos Santos Campos. Turma: 18122.1M
Blog realizado como requisito aliativo da matéria de matemática, III unidade, ministrado pelo prof. Mateus Souza de Oliveira.😁
Função Logarítmica
- A inversa da função exponencial é a Função Logarítmica.
- A função logarítmica é definida como f(x) = logax, com a real positivo e a ≠ 1.
- Sendo, o logaritmo de um número definido como o expoente ao qual se deve elevar a base a para obter o número x, ou seja, y = logax ⇔ ay = x.
Gráfico da Função Logarítmica
- O gráfico da função logarítmica é uma curva, construída em razão dos valores aplicados em x e os respectivos resultados calculados para f (x).
- As coordenadas são colocadas dentro do plano carteziano nos quadrantes I e II, pois essa função é caracterizada por x > 0.
- Além disso, a depender da base "a", são classificadas em crescente e decrescente.
Função crescente
- Caso a base a seja maior que 1 (x1 < x2 <---> loga x1 < loga x2), a função logarítmica é dita como crescente, já que à medida que x aumenta acontece o mesmo com o f(x). É uma curva que cresce em virtude do aumento de x.
- Quando estipulamos valores reais positivos para x e encontramos imagens, que podem ser todos os tipos de reais, inclusive os negativos,
- o gráfico crescente é da seguinte forma:

Função decrescente
- Se a base for 0 < a < 1, a função é decrescente em todo o seu domínio (x1 < x2<--->loga x1 > loga x2).
- Isso ocorre porque à medida que x aumenta, a imagem diminui.
- Essa relação inversamente proporcional origina a seguinte representação gráfica:

- Uma relação importante é que o gráfico de duas funções inversas são simétricos em relação a bissetriz dos quadrantes I e III.
- Desta maneira, conhecendo o gráfico da função exponencial de mesma base, por simetria podemos construir o gráfico da função logarítmica.
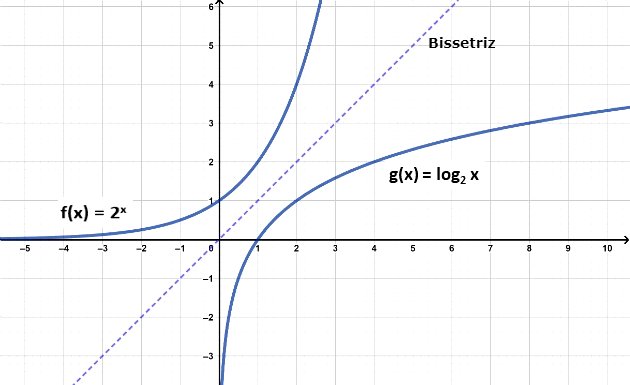
- No gráfico acima, observamos que enquanto a função exponencial cresce rapidamente, a função logarítmica cresce lentamente


Comentários
Postar um comentário