função quadrática
Aluna: Aislin Gabriella dos Santos Campos. Turma: 18122.1M
Blog realizado como requisito aliativo da matéria de matemática, III unidade, ministrado pelo prof. Mateus Souza de Oliveira.😁
FUNÇÃO QUÁDRATICA
A função quadrática, também chamada de função polinomial de 2º grau, é uma função representada pela seguinte expressão:
f(x) = ax2 + bx + c
Onde a, b e c são números reais e a ≠ 0.
Forma fatorada:
- do 2o grau para f(x) = ax2 + bx + c é f(x) = a(x-x1)(x-x2), onde x1 e x2 são as raízes da equação ax2 + bx + c = 0.
Exemplo 1:
Escreva na forma fatorada a equação x2 - 5x + 6 = 0.
Solução:
Calculando as raízes da equação x2 - 5x + 6 = 0, obtemos x1= 2 e x2= 3.Sendo a= 1, x1= 2 e x2= 3, a forma fatorada de x2 - 5x + 6 = 0 pode ser assim escrita: (x-2).(x-3) = 0
Como resolver uma função quadrática?
- Para resolver uma equação do segundo grau, há vários métodos, como a fórmula de Bhaskara e a soma e produto.
- As raízes de uma função quadrática são os valores de x que fazem com que f(x) = 0. Sendo assim, para encontrar as raízes de uma equação do 2º grau, faremos:
ax² + bx + c = 0.
Video explicando como resolver as funções:
https://youtu.be/Xv2QrQK9I7E
Exemplo 2:
f(x) = x² +2x – 3
a = 1
b = 2
c = –3
Formúla do delta:Δ =b² – 4ac
Δ=2² – 4 ·1·(-3)
Δ=4 +12
Δ = 16
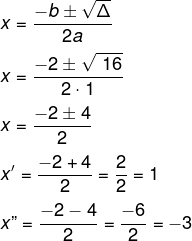
Então, os zeros da função são {1, -3}.
- Observe que a quantidade de raízes de uma função quadrática vai depender do valor obtido pela expressão: Δ = b2 – 4. ac, o qual é chamado de discriminante ou delta
Assim,
- Se Δ > 0, a função terá duas raízes reais e distintas (x1 ≠ x2);
- Se Δ , a função não terá uma raiz real;
- Se Δ = 0, a função terá duas raízes reais e iguais (x1 = x2).
Outro jeito de resolvermos a função quadrática, é por soma e produto. Segue um pequeno vídeo para vocês ficarem por dentro também:
https://youtu.be/z5V-S7Luinw
Gráfico da função quadrática
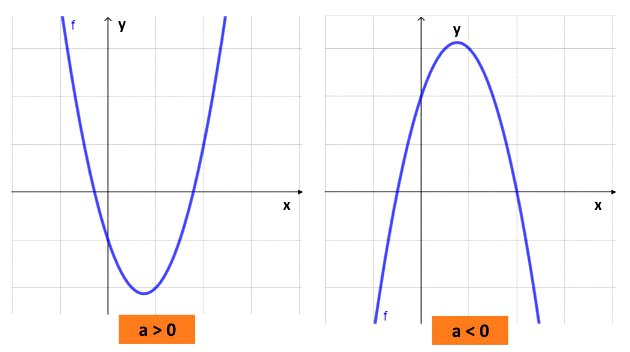
- O gráfico das funções do 2º grau são curvas que recebem o nome de parábolas.
- Diferente das funções do 1º grau, onde conhecendo dois pontos é possível traçar o gráfico, nas funções quadráticas são necessários conhecer vários pontos.
A curva de uma função quadrática corta o eixo x nas raízes ou zeros da função, em no máximo dois pontos dependendo do valor do discriminante (Δ). Assim, temos:
- Se Δ > 0, o gráfico cortará o eixo x em dois pontos;
- Se Δ = 0, a parábola tocará o eixo x em apenas um ponto.
- Existe ainda um outro ponto, chamado de vértice da parábola, que é o valor máximo ou mínimo da função.Este ponto é encontrado usando-se a seguinte fórmula:
- O vértice irá representar o ponto de valor máximo da função quando a parábola estiver voltada para baixo e o valor mínimo quando estiver para cima.
Fontes:
memes: google e pinterest
Livro de matemática conjuntos e funções- meu caderno de matemática
https://www.todamateria.com.br/funcao-quadratica/
https://www.somatematica.com.br/fundam/equacoes2/equacoes2_10_2.php
https://www.somatematica.com.br/fundam/equacoes2/equacoes2_10_2.php


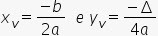
Comentários
Postar um comentário