Aluna: Aislin Gabriella dos Santos Campos.             Turma: 18122.1M

          

          Blog realizado como requisito aliativo da matéria de matemática, III unidade, ministrado pelo prof. Mateus Souza de Oliveira.😁 

Olá pessoal, a partir dessa publicação, iremos começar a aprender sobre funções.

FUNÇÃO AFIM

Chega na morena ou no moreno e manda:

HAHAHAHAHA, to brincando!

Mas voltando...

• Também chamada de função do 1º grau, é uma função f : ℝ→ℝ
•  Definida como f(x) = ax + b, sendo a e b números reais. 
•  O número a é chamado de coeficiente de x e representa a taxa de crescimento ou taxa de variação da função. Já o número b é chamado de termo constante.

 Polinomial  do  1º grau/ indentidade

•  É a mais simples;
•  F:R→R (reais em reais)
•  A função identidade, onde y = f(x) = x.  
• Sua fórmula:
• y = f(x) = ax + b
• Os valores do seu domínio são os mesmos da imagem do contradomínio.

Gráfico de uma Função do 1º grau

• O gráfico de uma função polinomial do 1º grau é uma reta oblíqua aos eixos Ox e Oy. 
•  Para construirmos seu gráfico basta encontrarmos pontos que satisfaçam a função.

Exemplo 1:

Construa o gráfico da função f (x) = 2x + 3.

Solução:

• Para construir o gráfico desta função, vamos atribuir valores arbitrários para x, substituir na equação e calcular o valor correspondente para a f (x).
• Sendo assim, iremos calcular a função para os valores de x iguais a: - 2, - 1, 0, 1 e 2. Substituindo esses valores na função, temos:

f (- 2) = 2. (- 2) + 3 = - 4 + 3 = - 1

f (- 1) = 2 . (- 1) + 3 = - 2 + 3 = 1

f (0) = 2 . 0 + 3 = 3

f (1) = 2 . 1 + 3 = 5

f (2) = 2 . 2 + 3 = 7

• Os pontos escolhidos e o gráfico da f (x) são apresentados na imagem abaixo:

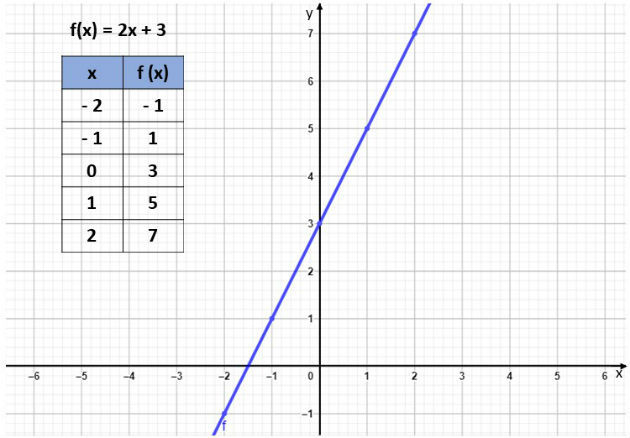
•  Para definir uma reta bastam dois pontos

💣Para facilitar os cálculos podemos, por exemplo, escolher os pontos (0,y) e (x,0). Nestes pontos, a reta da função corta o eixo Ox e Oy respectivamente.

Função Crescente e Decrescente

• Uma função é crescente quando ao atribuirmos valores cada vez maiores para x;
• Já a função decrescente é aquela que ao atribuirmos valores cada vez maiores para x, o resultado da f (x) será cada vez menor.

💣Para identificar se uma função afim é crescente ou decrescente, basta verificar o valor do seu coeficiente angular.

• Se o coeficiente angular for positivo, ou seja, a é maior que zero, a função será crescente. Ao contrário, se a for negativo, a função será decrescente.

Exemplo 2:

A função 2x - 4 é crescente, pois a = 2 (valor positivo). Entretanto, a função - 2x + - 4 é decrescente visto que a = - 2 (negativo). Essas funções estão representadas nos gráficos abaixo:

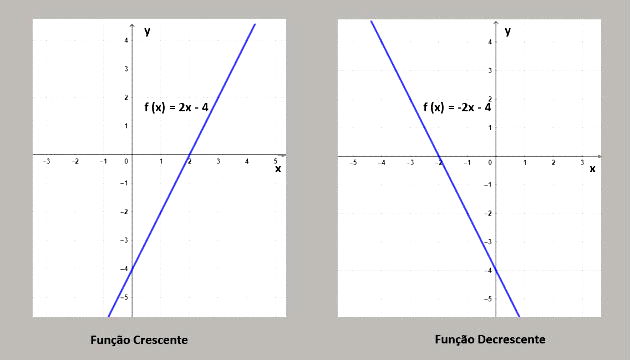
Coeficiente Linear e Angular

• Como o gráfico de uma função afim é uma reta, o coeficiente a de x é também chamado de coeficiente angular. 
• O termo constante b é chamado de coeficiente linear e representa o ponto onde a reta corta o eixo Oy. 

Exemplo 3:

Sendo x = 0, temos:

y = a.0 + b ⇒ y = b

• Quando uma função afim apresentar o coeficiente angular igual a zero (a = 0) a função será chamada de constante. Neste caso, o seu gráfico será uma reta paralela ao eixo Ox.

↓Abaixo representamos o gráfico da função constante f (x) = 4:

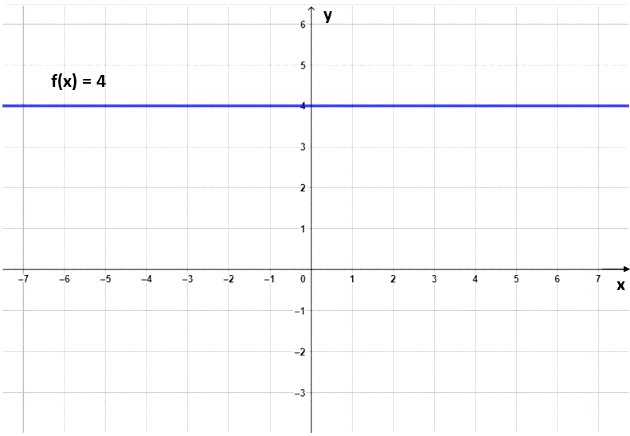
• Ao passo que, quando b = 0 e a = 1 a função é chamada de função identidade. O gráfico da função f (x) = x (função identidade) é uma reta que passa pela origem (0,0).
• Além disso, essa reta é bissetriz do 1º e 3º quadrantes, ou seja, divide os quadrantes em dois ângulos iguais, conforme indicado na imagem abaixo:

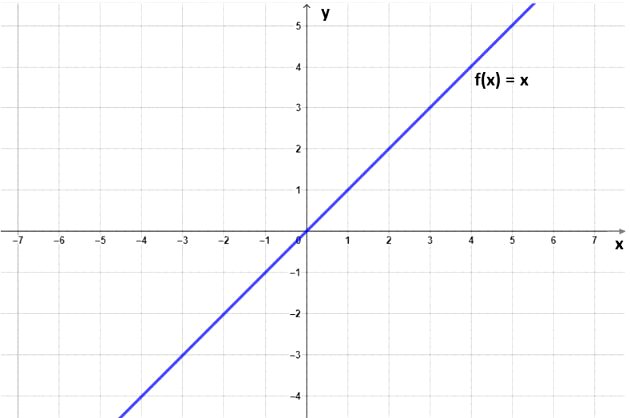
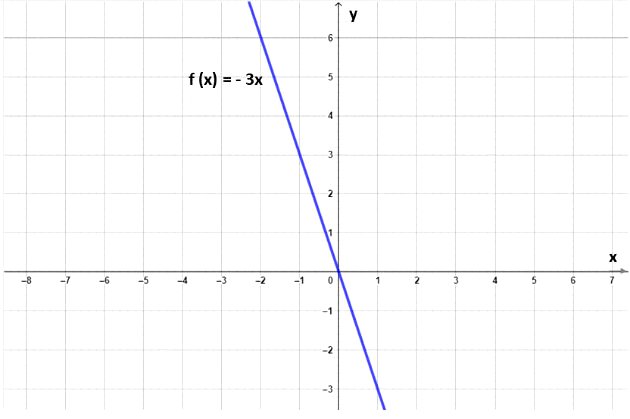
• Temos ainda que, quando o coeficiente linear é igual a zero (b = 0), a função afim é chamada de função linear. Por exemplo as funções f (x) = 2x e g (x) = - 3x são funções lineares.

💣O gráfico das funções lineares são retas inclinadas que passam pela origem (0,0).

Representamos abaixo o gráfico da função linear f (x) = - 3x:

  Função constante

• Diferencia-se das funções do 1° grau por não poder ser caracterizada como crescente ou decrescente, sendo, por isso, constante. 
• Podemos afirmar que uma função constante é definida pela seguinte fórmula:
• f(x) = c, c  
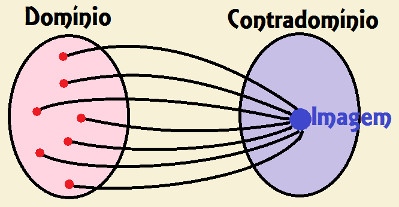
• A representação da relação estabelecida por uma função constante por meio do diagrama de flechas assemelha-se com a representação da imagem a seguir
• Independentemente dos valores pertences ao domínio, a imagem é sempre composta por um único elemento.

• O gráfico da função constante também apresenta uma particularidade em relação às demais funções. Ele é sempre uma reta paralela ou coincidente ao eixo x.

 

Exemplo 4:

f(x) = 2

O gráfico da função f(x) = 2 é uma reta paralela ao eixo x que intercepta o eixo y no ponto (0, 2).

Fontes: https://www.todamateria.com.br/funcao-afim/ os gráficos são do mesmo site.

https://www.educamaisbrasil.com.br/enem/matematica/funcao-identidade

https://mundoeducacao.uol.com.br/matematica/funcao-constante.htm

livro de matemática conjuntos e funções- meu caderno de matemática 

memes: https://br.pinterest.com/  e google