Introdução a lógica

             Aluna: Aislin Gabriella dos Santos Campos.             Turma: 18122.1M

          

          Blog realizado como requisito aliativo da matéria de matemática, III unidade, ministrado pelo prof. Mateus Souza de Oliveira.😁

INTRODUÇÃO A LÓGICA

  A lógica matemática analisa determinada proposição buscando identificar se representa uma afirmação verdadeira ou falsa.

   PROPOSIÇÕES:                    

• As proposições são palavras ou símbolos que expressam um pensamento com um sentido completo e indicam afirmações de fatos ou de ideias.
• Essas afirmações assumem valores lógicos que podem ser verdadeiros ou falsos e para representar uma proposição usualmente utilizamos as letras p e q.

         exemplos de proposições:                   

• Vasco é um clube carioca.                     
• Bolo de chocolate é gostoso.
• 7 < 4.
• 2 é ímpar. 

• Considerando a lógica matemática, uma proposição não pode ser ao mesmo tempo verdadeira e falsa. 
• As proposições podem ser simples, quando apresentam apenas uma sentença, e compostas quando são formadas pela combinação de duas ou mais proposições simples.
• "O céu é azul" é um exemplo de proposição simples;
•  já a sentença "O céu é azul e as nuvens são brancas" é um exemplo de proposição composta.

        CONECTIVOS:

• As proposições simples que formam uma proposição composta são ligadas por elementos que são chamados de conectivos.
•  Além disso, também podemos utilizar conectivos para modificar uma proposição.
•   Na proposição "O céu é azul e as nuvens são brancas" o elemento e é um conectivo que une duas proposições, já na proposição "O céu não é azul" o conectivo não modifica a proposição.

    Tabela Verdade

    

• Quando temos proposições compostas, os valores lógicos resultantes dependem única e exclusivamente dos valores de cada proposição simples.

• Diante disso, utilizamos um dispositivo chamado tabela verdade ou tabela de verdade, onde são colocados os valores de cada proposição e de acordo com os conectivos presentes chegamos ao valor lógico final.

    Operações Lógicas

• As operações feitas a partir de proposições são chamadas de operações lógicas.
• As operações lógicas fundamentais são: negação, conjunção, disjunção, condicional e bicondicional.

        Negação

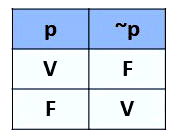
• Esta operação representa o valor lógico oposto de uma dada proposição. 
• Desta forma, quando uma proposição é verdadeira, a não proposição será falsa.

    Exemplo

        p: Minha filha estuda muito.                                   p
       ~p: Minha filha não estuda muito.

      Conjunção

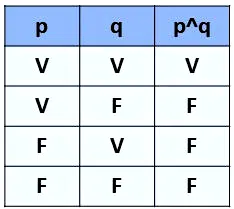
• A conjunção é utilizada quando entre as proposições existe o conectivo e. Esta operação será verdadeira quando todas as proposições forem verdadeiras.
• O símbolo utilizado para representar essa operação é o ^, colocado entre as proposições. Desta forma, quando temos p ^ q, significa "p e q".

Desta forma, a tabela verdade desse operador lógico será:

    Disjunção

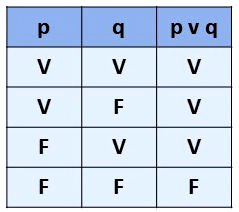
• Nesta operação, o resultado será verdadeiro quando pelo menos uma das proposições é verdadeira.
•  Sendo assim, será falso apenas quando todas as proposições forem falsas.
• A disjunção é usada quando entre as proposições existe o conectivo ou e para representar esta operação é usado o símbolo v entre as proposições, assim, p v q significa "p ou q".

    Condicional

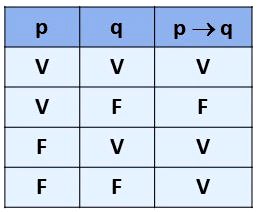
• A condicional é a operação realizada quando na proposição utiliza-se o conectivo se... então.... Para representar esse operador usamos o símbolo →. Assim, p → q significa "se p, então q".
• O resultado desta operação só será falso quando a primeira proposição for verdadeira e a consequente for falsa.

Exemplo

Qual o resultado da proposição "Se um dia tem 20 horas, então um ano tem 365 dias"?

Solução

Sabemos que um dia não tem 20 horas, logo essa proposição é falsa, também sabemos que um ano tem 365 dias, logo essa proposição é verdadeira.

Desta forma, o resultado será verdadeiro, pois o operador condicional só será falso quando a primeira for verdadeira e a segunda falsa, que não é o caso.

Bicondicional

• O operador bicondicional é representado pelo símbolo ⟺ e indica uma proposição do tipo ...se e somente se.... Portanto,  significa "p se e somente se q", ou seja, p é condição necessária e suficiente para q.
• Ao usar esse operador, a sentença será verdadeira quando as proposições forem ambas verdadeiras ou ambas falsas.

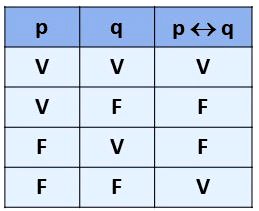
Exemplo:

Qual o resultado da proposição "30 = 2 se somente se 2 + 5 = 3"?

Solução:

A primeira igualdade é falsa, pois 30 = 1 e a segunda também é falsa (2 + 5 = 7), desta maneira, como ambas são falsas, então, o valor lógico da proposição é verdadeiro.

Fonte: https://www.todamateria.com.br/logica-matematica/#:~:text=A%20l%C3%B3gica%20matem%C3%A1tica%20analisa%20determinada,ou%20seja%2C%20em%20argumenta%C3%A7%C3%B5es%20v%C3%A1lidas. 

obs: as tabelas são do mesmo site.

Memes: https://br.pinterest.com/ e google .