Progressão Aritmética (concluido)
Aluna: Aislin Gabriella dos Santos Campos. Turma: 18122.1M
Blog realizado como requisito aliativo da matéria de matemática, III unidade, ministrado pelo prof. Mateus Souza de Oliveira.😁
Progressão Aritmética
- É uma sequência de números onde a diferença entre dois termos consecutivos é sempre a mesma. Essa diferença constante é chamada de razão da P.A..
- Sendo assim, a partir do segundo elemento da sequência, os números que surgem são resultantes da soma da constante com o valor do elemento anterior.
💣Isso é o que a diferencia da progressão geométrica (P.G.), pois nesta, os números são multiplicados pela razão, enquanto na progressão aritmética, eles são somados.
- As progressões aritméticas podem apresentar um número determinado de termos (P.A. finita) ou um número infinito de termos (P.A. infinita).
- Para indicar que uma sequência continua indefinidamente utilizamos reticências, por exemplo:
- a sequência (4, 7, 10, 13, 16, ...) é uma P.A. infinita.
- a sequência (70, 60, 50, 40, 30, 20, 10) é uma P.A. finita.
Classificação de uma P.A.
De acordo com o valor da razão, as progressões aritméticas são classificadas em:
- Constante: quando a razão for igual a zero. Por exemplo: (4, 4, 4, 4, 4...), sendo r = 0.
- Crescente: quando a razão for maior que zero. Por exemplo: (2, 4, 6, 8,10...), sendo r = 2.
- Decrescente: quando a razão for menor que zero (15, 10, 5, 0, - 5,...), sendo r = - 5
Propriedades da P.A.
1ª propriedade:
Em uma P.A. finita, a soma de dois termos equidistantes dos extremos é igual à soma dos extremos.
Exemplo 1:
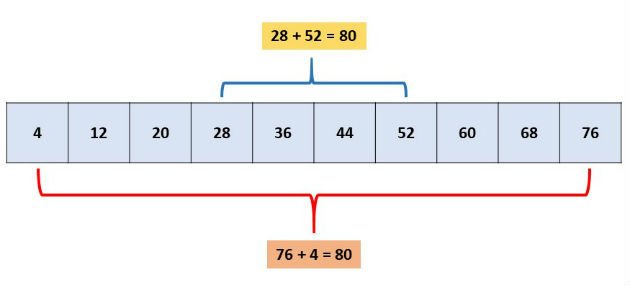
2ª propriedade:
Considerando três termos consecutivos de uma P.A., o termo do meio será igual a média aritmética dos outros dois termos.
Exemplo 2:
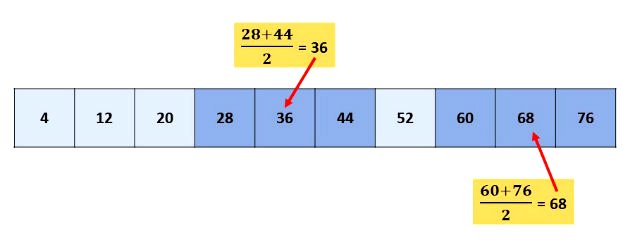
3ª propriedade:
Em uma P.A. finita com número de termos ímpar, o termo central será igual a média aritmética entre termos equidistantes deste. Esta propriedade deriva da primeira.
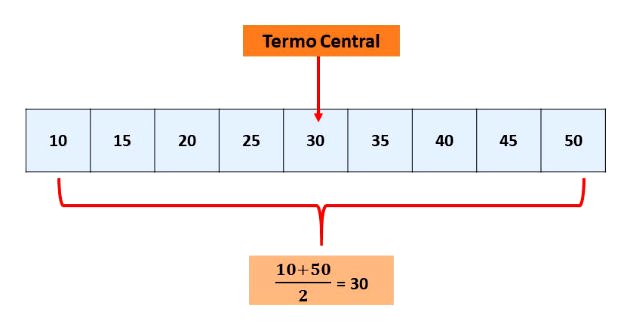

.jpeg)
Comentários
Postar um comentário